Studying Atropisomerism with Dihedral Scans
In this tutorial, we'll use Rowan to conduct a dihedral scan on a hindered biaryl compound, locate the transition state for atropisomer interconversion, and predict the barrier to rotation.
Heads up! Since we released this tutorial, we've added support for a variety of neural network potentials, which are much faster and probably more accurate than the methods used here. We recommend using AIMNet2 for this tutorial, although we haven't re-run all the calculations yet. We have also deprecated support for running jobs with HF-3c.
Background
Atropisomerism occurs when hindered rotation around a single bond gives rise to different stereoisomers. In a recent review, Jeffrey Gustafson and co-workers discussed the increasing importance of atropisomers and atropisomerism in pharmaceutical compounds: according to their research, "∼30% of recent FDA-approved small molecules (2010–2018) possess at least one class-1 atropisomeric axis." In many cases only one atropisomer is biologically active, while the other atropisomer contributes to off-target activity or toxicity.
In a 2013 paper, Steven LaPlante and co-workers divided atropisomers into three classes based on their barrier to rotation. Atropisomers with a high barrier to interconversion (class 3) will behave as entirely separate compounds, while atropisomers with a low barrier to interconversion (class 1) will rapidly sample many different conformations. Atropisomers with middling barriers to rotation (class 2) interconvert on similar timescales to other pharmacokinetic processes: accordingly, "special caution is warranted" (LaPlante).
Understanding the barrier to atropisomer interconversion is very important when considering compounds with a potential atropisomeric axis: otherwise, atropisomerism can be "a lurking menace" (to quote one review) which can lead to numerous problems later on in drug development. Successful drugs have been developed in all three classes of LaPlante's classes, but it is important to understand which class a given molecule belongs to: class 3 atropisomers should be prepared in isomerically pure form, while class 1 atropisomers cannot be isolated and are administered as a mixture.
While it's possible to measure the rate of atropisomer interconversion in the laboratory through various methods (as described in this article), it is often faster and easier to predict the barrier to rotation using computational chemistry. Quantum chemical calculations are commonly used to generate conformational energy profiles for potentially atropisomeric compounds, and the agreement with experiment is generally excellent.
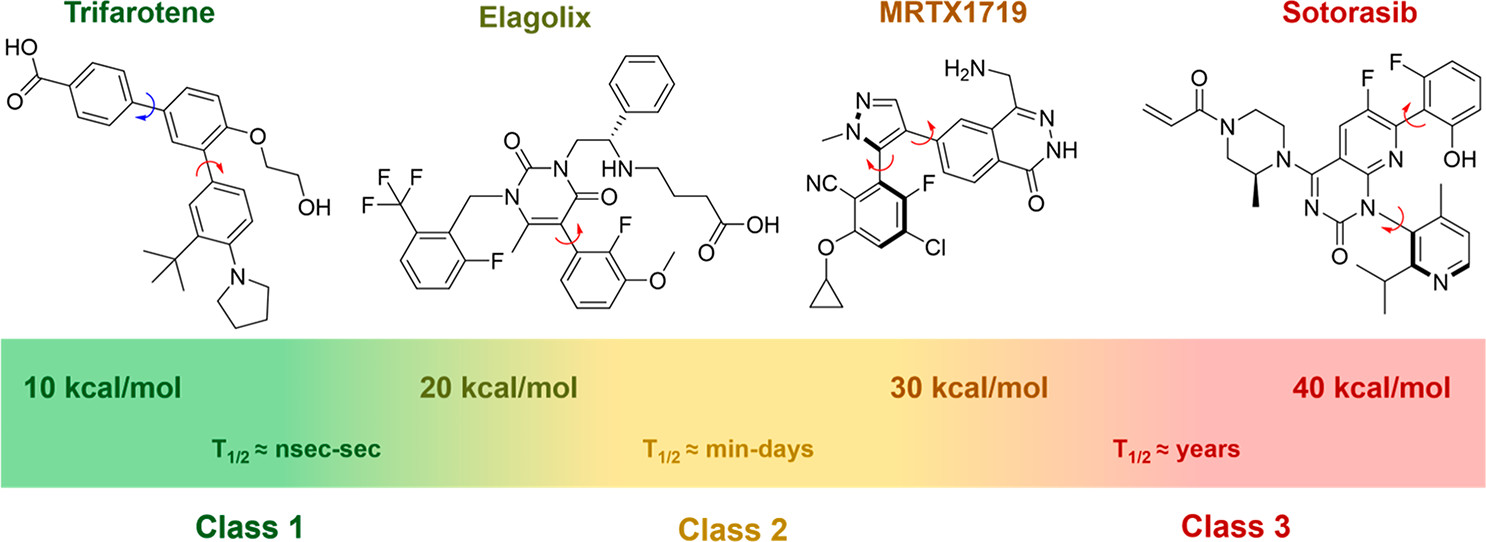
In this tutorial, we'll use Rowan to predict the barrier to rotation for a RORγt inhibitor investigated by Novartis as a potential treatment for inflammatory and autoimmune diseases like psoriasis and arthritis. In the Novartis work, high-throughput screening identified N-aryl imidazoles as a promising hit, and further optimization led to the development of compounds bearing 2,6-dichlorophenyl rings (3–5). Efforts to improve ADME properties through modification of the core (6-7) substantially reduced binding affinity, and so substitution at the 3 position of the dichlorophenyl ring was considered next.
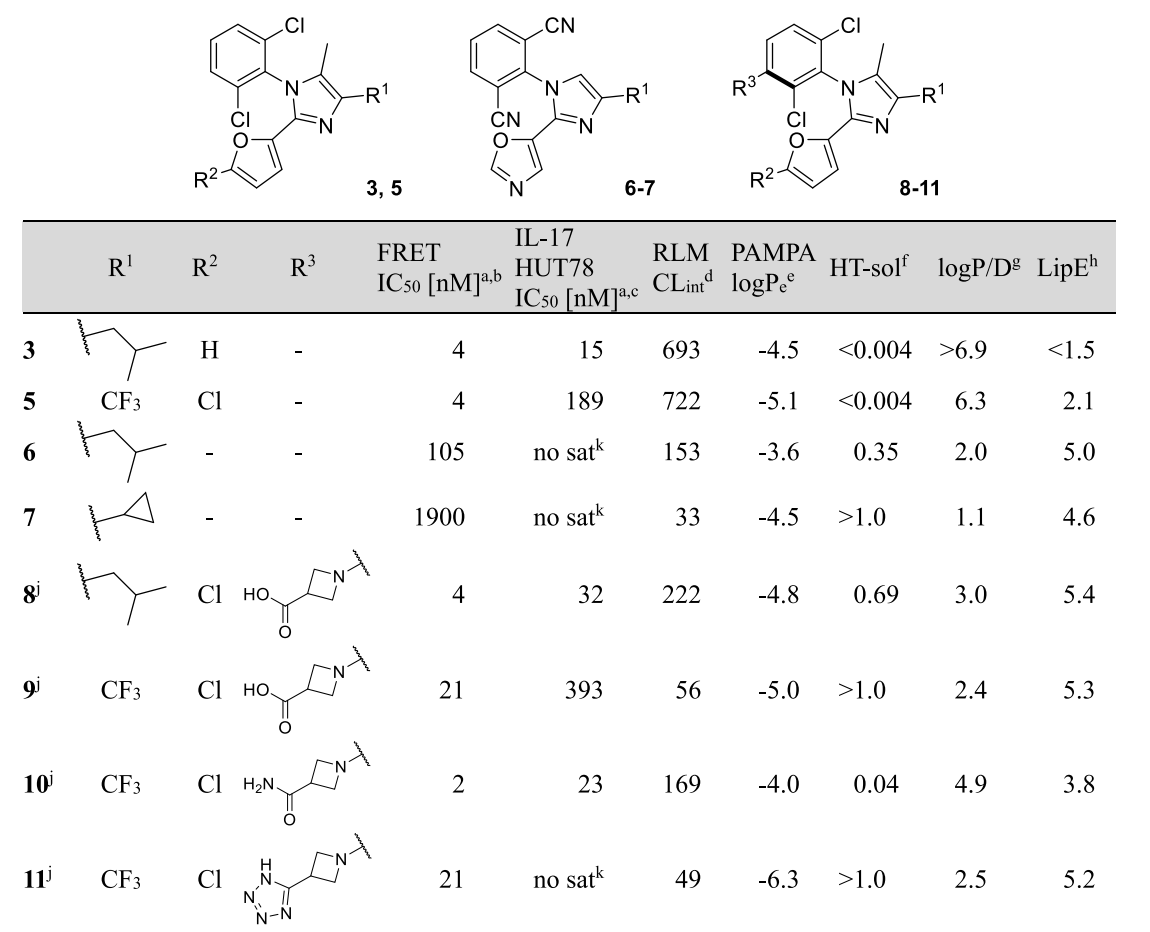
The authors anticipated that these compounds might exhibit hindered rotation around the aryl–aryl C–N bond. To predict if the resulting compounds (8-11) would be formed as multiple separable atropisomers, the authors conducted quantum chemical calculations to determine the barrier to rotation. In this tutorial, we will demonstrate how to do this for compound 5.
Running a Dihedral Scan
To start, we need to generate a structure for compund 5.
We can do this by drawing the structure in ChemDraw, highlighting it, and then clicking "Edit > Copy As > SMILES" from the menu to obtain the SMILES string corresponding to the structure we've drawn.
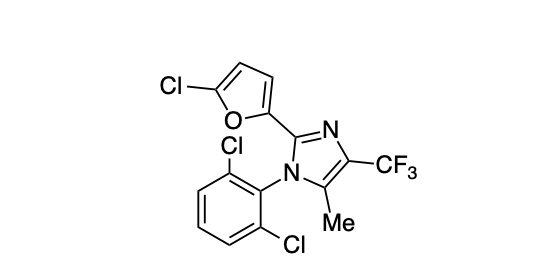
When I do this, I get ClC1=C(N2C(C)=C(C(F)(F)F)N=C2C3=CC=C(Cl)O3)C(Cl)=CC=C1, which isn't quite canonical SMILES but will work well enough for our purposes.
Here's the ChemDraw structure that gave this SMILES string:
We can then use this SMILES string to load compound 5 into Rowan. Go to labs.rowansci.com/new/scan, click "Input Smiles," and paste in the string from ChemDraw. Your screen should look like this:
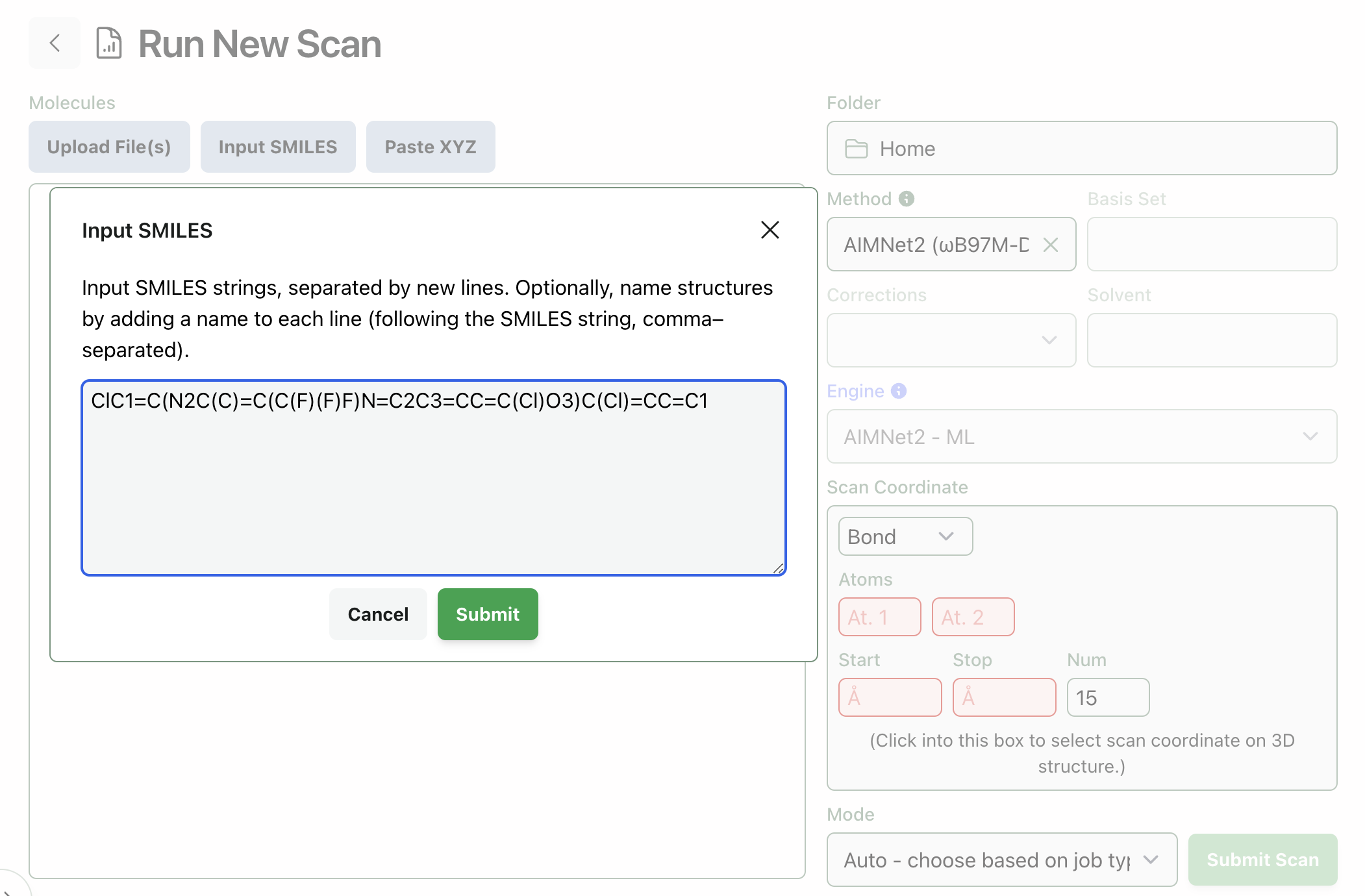
When you click "Submit," Rowan will automatically convert the SMILES string provided into a 3D structure and display it on the screen. Take a look at the structure this generates and verify that the SMILES conversion worked properly.
Now we need to run a dihedral scan on this structure. To do this, click into "Scan Coordinate" box and configure a dihedral scan about the C5–N4–C3–C2 dihedral angle from 0º to 360º with 15 steps. (These atom numbers were chosen by clicking on atoms in the structure: you can select any four atoms to see the dihedral angle. There are several choices of atom numbers that are all equally good here.)
The other settings are straightforward: we'll leave the method to HF-3c, a good default for this sort of task, and choosing a scan means that "Optimize" is pre-selected as our task. We are ready to submit our job! At this point, your screen should look like this:

After clicking "Submit Scan," you'll be redirected to the scan view; the scan will take a few hours to run.
Here's the completed scan: click through the different steps (or press the arrow keys) to visualize the different structures. We can immediately see that the barrier to rotation will be quite high: for instance, the point where the C5–N4–C3–C2 dihedral is 180º (step 8/15) has an energy about 37 kcal/mol above the lowest structure sampled. So, we can conclude based on this scan that the atropisomers will be separable compounds (LaPlante class 3) and will not interconvert after isolation or in vivo.
(You can click "View in Rowan" to open the scan in a new tab and view the individual calculations.)
Locating the Ground State
The scan we ran above gives us a quick sense of what the barrier to rotation will be, and often only a scan is needed to predict what class a given atropisomer will belong to: LaPlante recommends this approach. Sometimes, however, we want to compute an actual rotational barrier, to compare to other analogues or to experimental data. To do this, we must first locate the ground and transition states for bond rotation.
The ground state is quite simple to find. Select the lowest energy point from the scan—in this case, step 5, where the CN–N4–C3–C2 dihedral is 102.8º—and click "Resubmit" and then select "Resubmit as calculation." Select the "Optimize" and "Frequencies" tasks, leaving everything else the same. Your screen should look like this (you can rename the calculation now, if you want, or later):
In my hands, this calculation finishes in a little over two hours. We can verify that the structure is indeed a true ground state by checking the frequencies tab and validating that there are no imaginary frequencies: all values are positive. Calculating the vibrational frequencies also gives us thermochemical values (viewable under the "Thermochemistry" tab), which will allow for calculation of the free energy rotational barrier.
Here's the structure: as before, you can view in a new tab by clicking "View in Rowan."
Locating the Transition State
Transition states are, in general, substantially more difficult to locate than ground states. For atropisomers with low barriers to rotation, the highest point from the scan is often a decent approximation to the transition state: unfortunately, this rotation is difficult enough that the high-energy scan points distort the rings to satisfy the dihedral constraint rather than actually getting close to the rotational transition state. (There is a lot of theory about why this occurs: see for instance this excellent paper by Jerzy Ciosłowski and Leo Radom.)
Here's what happens when you try to resubmit one of the high-energy scan points (this was step 8/15 from above). You can see that the molecule collapses to a low-energy conformation and eventually locates a transition state for methyl rotation—a common failure mode for TS calculations. (This calculation was allowed to finish for pedagogical purposes, but it was obvious after about 15 minutes that this wasn't going to succeed; the job could safely have been canceled.)
Fortunately, we have some chemical intuition about what the TS should look like: we expect the two rings to be parallel, not perpendicular, since the TS ought to connect the two atropisomers.
We can thus download the ground-state structure as an .xyz file and use Avogadro or another program to manually rotate the C–N bond to make the two rings parallel, rotating the furan a bit to avoid any short interatomic distances.
Then, we can re-upload the structure to Rowan, add dihedral constraints to force the two rings to remain parallel, and submit a constrained optimization.
The initial structure is pretty rough, but after about an hour the optimization converges towards something that looks more like a transition state:
This structure looks like what we might expect from a TS, and moreover qualitatively matches other dihedral rotation transition states from the literature (compare to Figure 7 here). Since it seems like we're pretty close, we can go ahead and resubmit this geometry as a transition state: remove the dihedral constraints, select the "Optimize (TS)" and "Frequencies" tasks, and click "Submit."
After a few hours, we locate the transition state. or any transition state, it's important to confirm that there is only one imaginary frequency, and that the frequency corresponds to the process we expect: here, there's a 45 cm-1 mode which corresponds to C3–N4 bond rotation, which is exactly what we've been looking for. (You can visualize this by clicking on the row under the Frequencies tab, increasing the amplitude, and rotating the structure so you're looking along the C–N bond axis.)
Computing the Barrier to Rotation
With our ground state and transition state in hand, we can now compute the barrier to rotation. The Gibbs free energy of the ground state is -2419.7661929 Hartree, and the Gibbs free energy of the transition state is -2419.6627466 Hartree, so the barrier can be computed as follows:
∆G‡ = (GTS - GGS) = (-2419.6627466 - -2419.7661929) * 627.509 (kcal/mol)/Hartree = 64.91 kcal/mol
This is really high! We can be confident that these atropisomers will not interconvert.
Correcting Single Point Energies
If we want to be even more precise, we can do a single-point energy correction at a higher level of theory. The idea behind single-point energy correction is that while electronic energies are quite sensitive to the level of theory employed, vibrational frequencies and geometries are much less sensitive. So, while we might not be able (or willing) to compute vibrational frequencies and get Gibbs free energy values at a high level of theory, we can approximate high-level Gibbs free energies by adding a low-level frequency correction to a high-level energy.
This is very easy to do in practice: resubmit both the ground and transition states and run energy calculations at the B3LYP-D3BJ/pcseg-1 level of theory (without optimization). These calculations take only a few minutes to complete: here's the ground state and the transition state. Then, add the energy from the B3LYP calculations to the "Gibbs Free Energy Corr." (under Thermochemistry) from the HF-3c calculations.
GGS ~= -2441.1257057 + 0.1842377 = -2440.9414680 Hartree
GTS ~= -2441.0419856 + 0.1856065 = -2440.8563791 Hartree
∆G‡ = (-2440.8563791 - -2440.9414680) * 627.509 = 53.39 kcal/mol
We can see that there's a substantial difference from above—unsurprising, given that HF-3c was not developed for barrier heights—but that the barrier remains very high. If we want to convert our ∆G‡ into a half-life, the math is simple, but even simpler is this free online calculator. Even at a temperature of 500 K, a barrier of 53.39 kcal/mol implies a half-life of over 450 years!
To be even more precise, we could perform a full optimization and frequency calculation at the B3LYP-D3BJ/pcseg-1 level of theory, starting from our HF-3c structures. A solvent model would help, as would additional single-point energy calculations with a triple-zeta basis set: as frequently found in computational chemistry, it's a question of how precise an answer is needed to give insight into the question at hand.